Zeno's Paradox and the Basis of Finance
How a 2,500 year old riddle hides many of the concepts that we use in the modern financial world
When I was a young Padawan and was learning the ways of the force mathematics, one of my professors discussed with me and my fellow students one of Zeno’s paradoxes, called Achilles and the tortoise (or, briefly, Achilles). It is a paradox that is often presented in relation to series, the mathematical operation of adding an infinite sequence of numbers.
Zeno of Elea was a Greek philosopher that lived approximately 2,500 years ago. A number of paradoxes on the motion of objects were attributed to him by Aristotle in his book Physics. The paradox of Achilles, in particular, highlights an apparently simple concept, yet so profound that it took more than two millennia to be formalized, thanks to the study of limits. This concept is that the sum of an infinite number of terms can produce a finite result.
Racing the tortoise
But let’s introduce the paradox proper first. The hero Achilles decides to challenge a tortoise to a speed race. Because he knows he’s much faster, and to make the competition more challenging, he’s giving the tortoise a head start. So, he’s going to start the race only after the tortoise has already covered some distance.
Now, by the time Achilles has covered this first distance, the tortoise itself will have covered some additional, however small, distance. By the time Achilles has covered this additional distance, the tortoise will have covedered yet another, smaller, distance. And so on.
The paradox is: how can we reconcile the obvious fact that Achilles is going to eventually reach the tortoise in a finite time with the fact that, in doing so, he’s going to have to cover an infinite sequence of distances?
The answer is that the sum of an infinite sequence of distances does not necessarily correspond to an infinite distance, and in fact it can be covered in a finite time. To see that, let’s assume that Achilles begins his race only after a time τ has passed since the tortoise first moved forward. Then it can be easily seen that the time it takes Achilles to cover the j-th step in the sequence described above is
Where clearly the term in parentheses is less than unity, because the tortoise is slower than Achilles. Therefore, the time it takes Achilles to reach the tortoise is the sum of all these times, from the start of the race to infinity
The summation on the right-hand side is known to be a geometric series. It is not different from the kind of exponential progressions that we sadly came to experience during the Covid pandemic, with one key difference. While the number of infected people grows exponentially, in this case the terms of the series decrease exponentially. This is due to the fact we noted above, that the term in parentheses is smaller than unity.
And herein lies the trick. When the individual terms of the series become smaller and smaller at a fast enough pace - as in this case - the summation of an infinite sequence converges to a finite quantity. Specifically, it can be shown that the sum of a converging geometric series equals to
Applying this to the previous result (but please note that this summation starts in 0, not in 1, so we need to subtract the first term from it) we easly obtain that
And this, by the way, is exactly the result you get by applying simple kinematics to the same problem. So, we have resolved the paradox.
Discounting cash flows
Geometric series have widespread applications in all domains, but one in particular where they come up all the time is finance. Consider, for instance, a perpetuity. A perpetuity is a contract that you can buy whereby who’s selling it is going to give you a certain amount of money, constant every year, forever.
So, how much should you pay for a perpetuity? What value do you assign to a constant flow of money that lasts forever? Obviously this cannot be infinite, because otherwise no one would buy it.
Well, like many things in finance, the present value of a perpetuity is the sum of its discounted cash flows. If the contract entitles you to an amount m of money every year then the present value of the payment that occurs on the j-th year is given by
In the equation above, r is the interest rate, assumed to be constant. Now you need to sum the present value of all payments from the first to infinity. So, the present value of the perpetuity is
Looks familiar, right? This is nothing but the geometric series we’ve already encountered in the paradox of Achilles. We already know that the sum of the series shall be finite, and specifically it leads us to to an incredibly simple result
This is the present value of a perpetuity. The figure below shows what fraction of this present value you get by including only a finite number of terms in the summation of future cash flows.
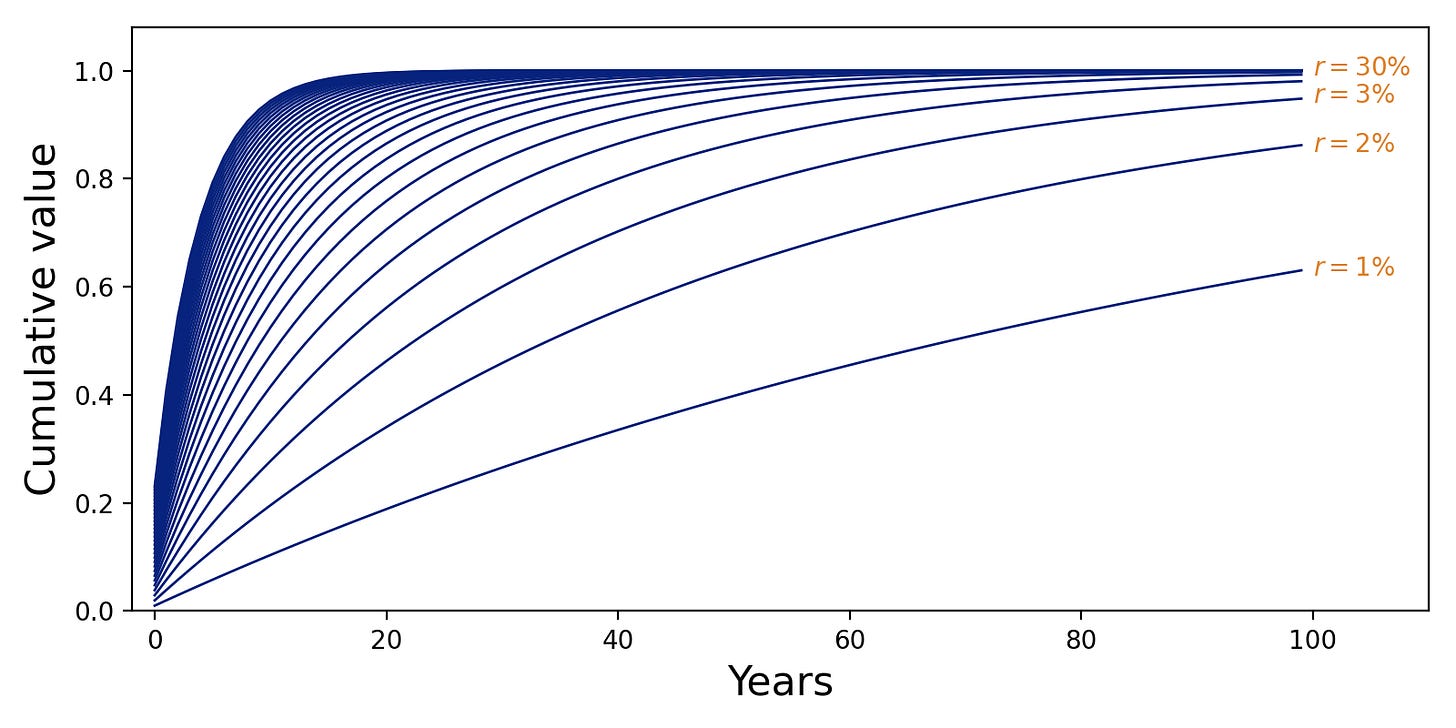
We can take this a step further, and use the same result to compute the present value of an annuity. An annuity is like a perpetuity, but the cash flow stops after a given number k of payments.
Clearly, the value of an annuity can be found by subtracting from the value of a perpetuity the value of another perpetuity that begins after k years, discounted to present. Mathematically
Or, by pulling out the present value of the perpetuity (this is how it’s commonly written in textbooks)
These same concepts lead one to calculating the present value of coupon bonds and mortgages. So, one may argue that a good portion of the modern financial system is based on the notion of converging geometric series, a notion that Zeno had implicitly grasped (but not explained) 2,500 years ago.
Of course, when it comes to the real world, one needs to take into account the fact that interest rates are random variables, rather than constants, so there is a need to model probabilities and risk - in other words you need to do all the things that make modern finance interesting. But this is a different story.
Thanks for reading this piece.